在完成robotics fundamental week3作业的时候，我发现要求求正向动力学矩阵，但是在绘制workspace的代码中并没有体现，而是使用了常规的没有难度的几何法，我想肯定是有联系的。

这样的联系应该就是：Forward kinematics homogeneous matrix表示了rotation和translation的关系（如图），利用此矩阵和最后一个frame中end-effector的相对坐标齐次矩阵相乘的结果是绝对坐标，也就是几何法求出来的坐标。

老师只讲了理论知识，没有进行case studies，所以我在理解这个的时候因为各种小错误还开始怀疑起理论。通过本文，我补充没有完成过的case studies，以此夯实基础。

思考

鉴于计算结果不一致，思考以下问题：

1. DH frame应怎么构建，尤其是X轴方向
2. DH参数如何取值
3. End-effector相对坐标如何表示

这些都是DH convention中我暂时不确定的地方，确定之后，应该可以计算出一致的结果。

Case Studies

RR serial manipulator

下面来看一个分析方法案例，思考这样分析有什么问题？

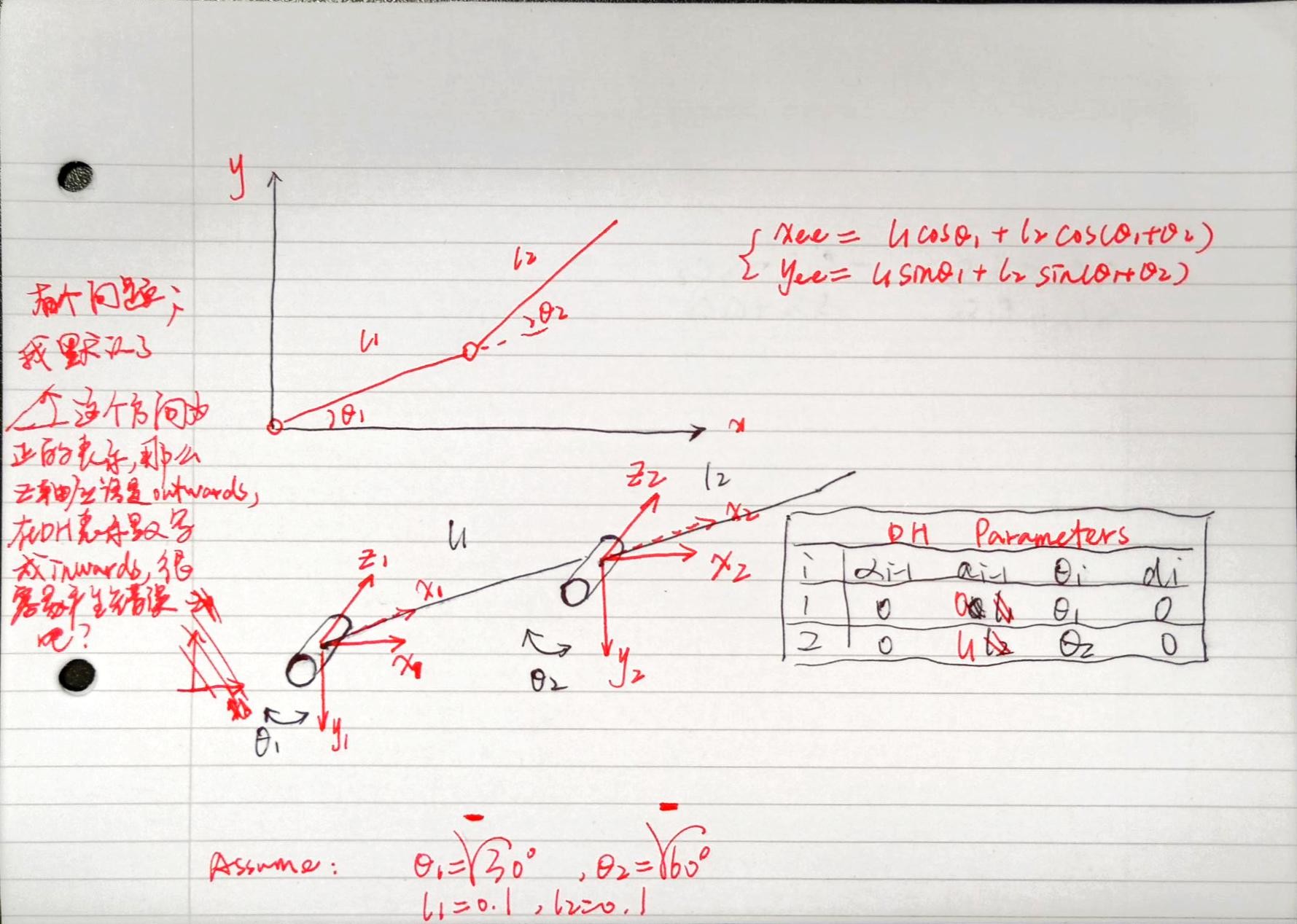
可以看出，我已经在纸上写出来了，问题就是出在Z轴选取方向以及X轴方向（emmm都错了很惭愧，说明case studies的重要性了）。我们对于旋转角的正负是有默认的规定的。那就是：

俯视旋转轴，或者规定旋转轴为垂直纸面向外，其余两个坐标轴的平面绕旋转轴逆时针旋转时，规定旋转角为正。

上面的分析案例，就是把Z轴规定到反向了。我们回归到文章开头说的思考问题。第二个问题中，DH参数的选择因此必须加上负号，这是错误的，必须为正号。然后由于X轴方向不正确，会导致end-effector的相对坐标写错。至于为什么，接着看正确案例。

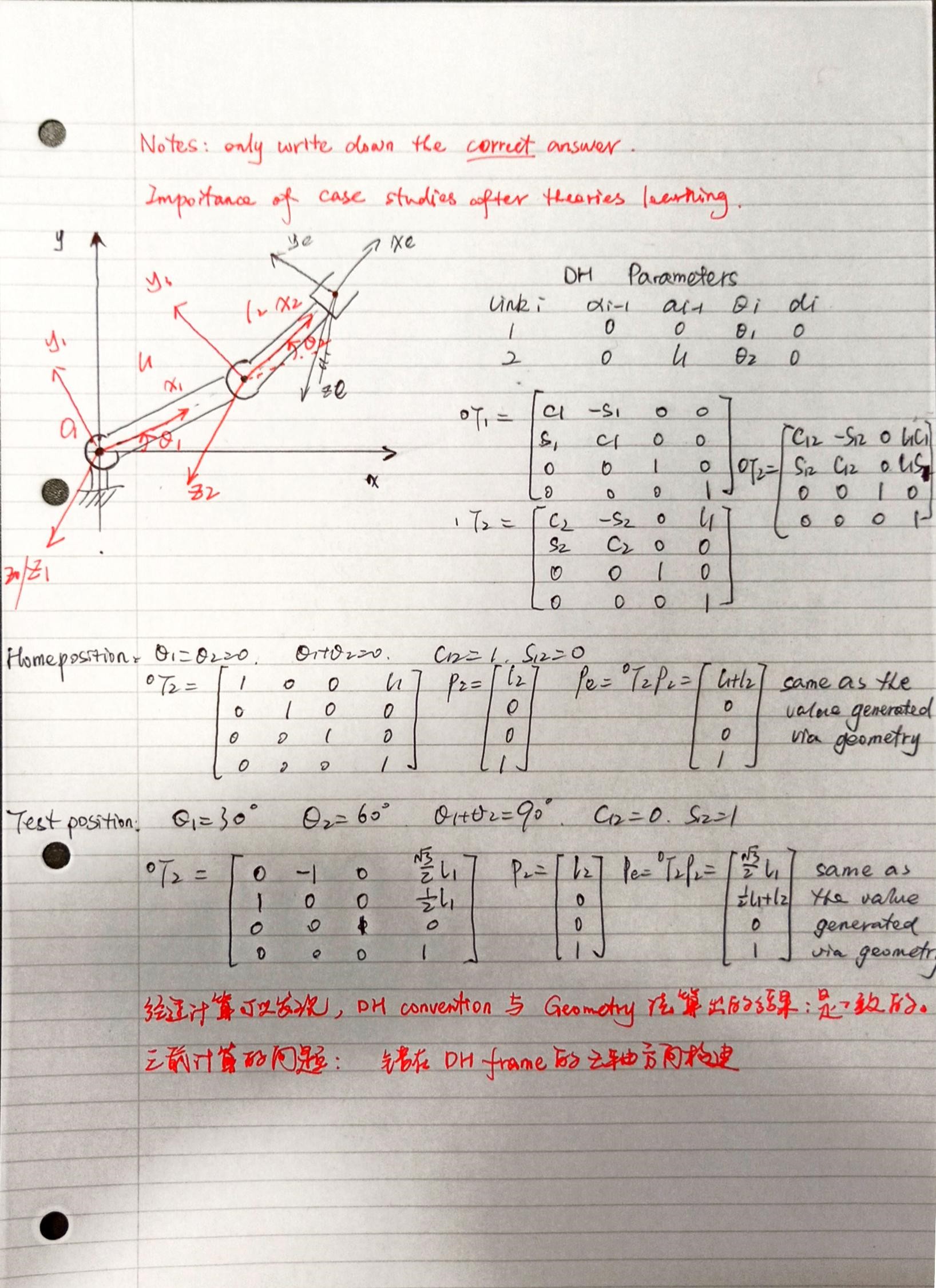
这才是正确的DH convention解决过程。

重新看两个重要的DH frame构建原则（也是容易犯错的两个原则）：

1. $Z_0$最好是和$Z_1$一致，避免分析混乱

   The base frame {0} is arbitrary. For simplicity chose $Z_0$ along $Z_1$ axis when the first joint variable is zero.

2. $X_0$沿着$Z_i$和$Z_{i+1}$之间的公共法线，而不是看$\theta$是不是0哦！

   Assign $X_i$ axis pointing along the common normal ($a_i$) in the direction from $Z_i$ axis to $Z_{i+1}$ axis. In the case of $a_i=0$, $x_i$ is normal to the plane of $Z_i$ and $Z_{i+1}$ axes.

解决了规范性问题，然后我把DH 矩阵的MATLAB代码写错了……

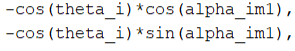
这两个应该是正号，现在想来应该是这里写错了，Z/X轴和相对坐标我的表示只要能自圆其说就可以了吧。不过还是按照上述正确标准来做。

RRRR serial manipulator

回到4R manipulator分析（下图是不正规的建模，现在开始就算做是不正确的）：

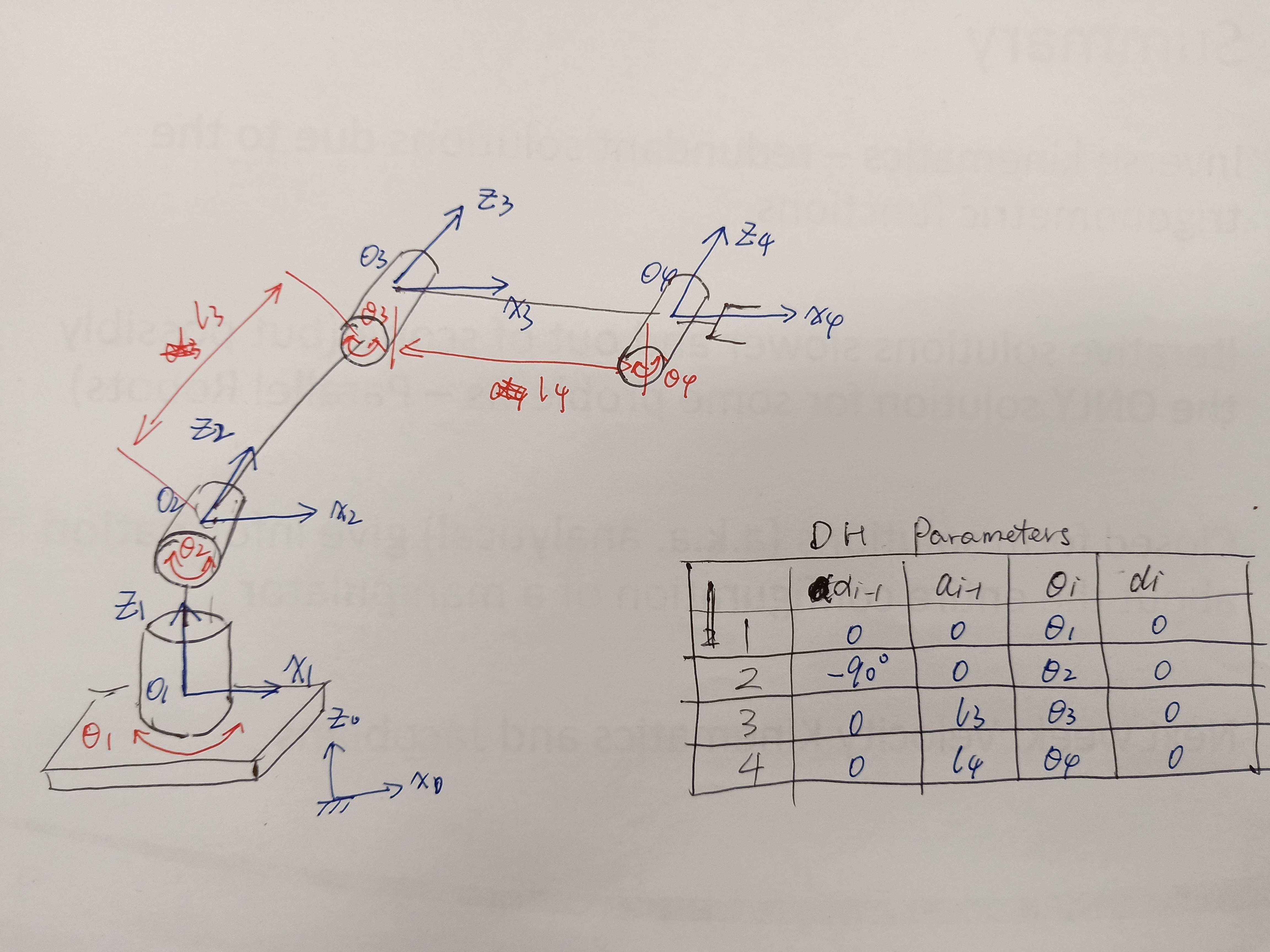
正确建模为：

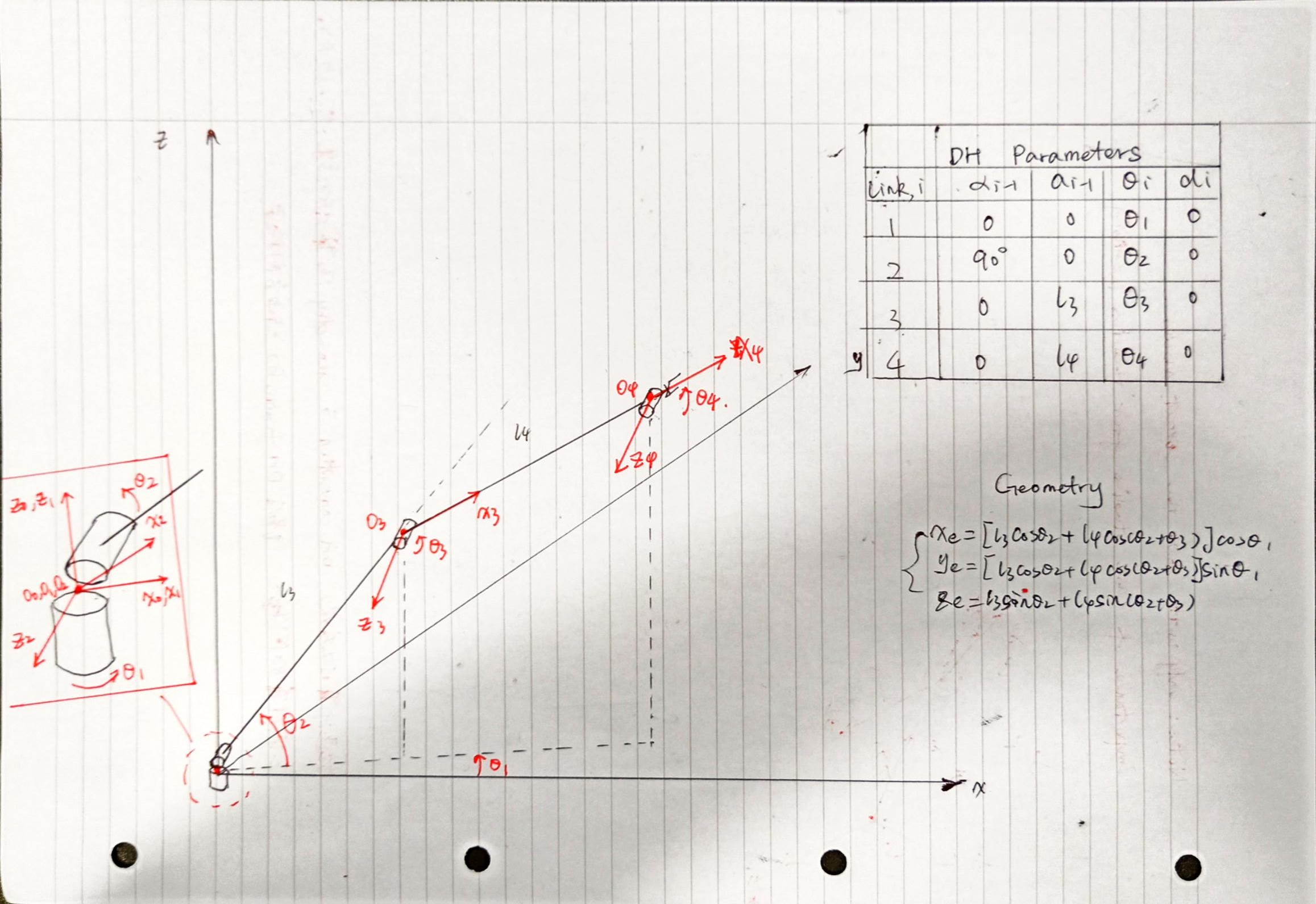
算不出正确结果？？？是这里代码错了

90/pi*180，我写的啥代码啊。。。以后还不如90/180*pi这样好看懂。

现在都一样了。

Case studies conclusion

总结一下，出现的什么错误才是致命错误：

1. 代码写错了（角度表示，方向和角度制转换）
2. DH convention的Z/X轴及角度和Geometry未统一

那以后写代码要注意什么？

• 首先建模一定要正确，图形要画好，大方，规整，色彩分明

对于代码的格式，我已经做得很不错了。改进一点：

• 矩阵数据要利用tab排成矩阵型

MATLAB 代码 (RRRR)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

% File:   CalcFK.m
% Name:   Jinhang Zhu
% Date:   25 Oct. 2019
% Email:  lm19073@bristol.ac.uk
% Descr:  Calculate the homogeneous transformation matrix for modified DH convention.

%% test 4R serial manipulator DH matrix
theta_1 = 20*pi/180;
theta_2 = 90*pi/180;
theta_3 = 30*pi/180;
theta_4 = -45*pi/180;
l3 = 0.1;
l4 = 0.1;
%   DH parameters table
% ---
%           alpha i-1   a i-1       theta i             d i
% ---
DH_param = [0,          0,          theta_1,            0;
            90*pi/180,  0,          theta_2,            0;
            0,          l3,         theta_3,            0;
            0,          l4,         theta_4,            0];
%   Matrix
FK_mat = modified_DH_whole(DH_param);
%   Note that the end-effector position in frame 4 is at origin
Pe = [0,0,0,1]'; 
Pe_DH = FK_mat *Pe;

%% test geomerical location
x_ee = (l3*cos(theta_2)+l4*cos(theta_2+theta_3))*cos(theta_1);
y_ee = (l3*cos(theta_2)+l4*cos(theta_2+theta_3))*sin(theta_1);
z_ee = l3*sin(theta_2)+l4*sin(theta_2+theta_3);
xyz_ee = [x_ee,y_ee,z_ee];

%% compare
disp('From DH convention');
Pe_DH(1:3,:)
disp('From Geometry');
xyz_ee'

函数代码详见：